La trigonometrie du cercle
Un radian c'est quoi ?
Il s'agit du rayon que l'on va courber afin de le faire correspondre à l'arc de cercle allant d'un point du cercle et de la longueur du rayon.

- $2\pi r $ = la circonference du cercle = $360 ° $ = $ 2 \pi rad $
- $\pi r $ = la moitié de la circonference du cercle = $180 ° $ = $ \pi rad $
Ce qui nous amène à penser que si : $$2\, \pi\, rad = 360^{\circ}$$ $$\pi\, rad = 180^{\circ}$$
Alors les équations suivantes sont également vraies : $$1\, radian = \frac{180}{\pi} = 57.2957795131 \,degrees$$ $$1\, degree = \frac{\pi}{180} = 0.01745329251 \, radian $$
Cosinus
Le $cosinus$ est un segment dont le point de depart est l'origine et se terminant en un point se situant sur l'axe des abscisses à l'intérieur du cercle.
Il est compris dans le diamètre du cercle.
La notion de $cosinus$ n'a de sens que pour retrouver la valeur d'un angle ou la longueur d'un arc de cercle.
Pour cela on utilisera l'$arccos$.
Par exemple dans un cercle de rayon 2, le $cos(1)$ se situera à la moitié de ce rayon du côté positif des abscisses.
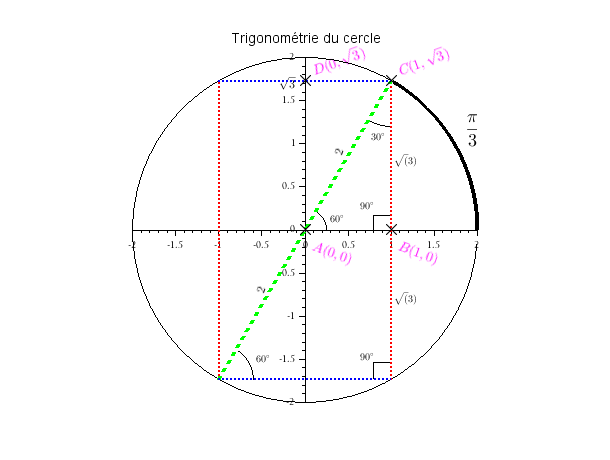
Sur l'image ci-dessous, on a les points suivants en rose : $$A(0, 0)$$ $$B(1, 0)$$ $$C(1, \sqrt{3})$$ $$D(0, \sqrt{3})$$
Le segment $[AB]$ represente le $cosinus$ de l'angle $\hat{BAC}$.
Ce dernier vaut $60^{\circ}$.
Pour plus de simplicite, dénommons cet angle $\theta$ represente par la lettre grecque theta ($\theta$).
Donc l'angle $\theta$ vaudra $cos(\theta)$ soit : $$cos(\theta) = \frac{cote\,adjacent}{hypothenuse}$$ Soit : $$cos(\theta) = \frac{1}{2}$$
Ceci nous donne un nombre qui est compris entre -1 et 1.
Donc $$-1 < cos(\theta) < 1$$
Dans notre cas pratique, on a : $$cos(\theta) = \frac{1}{2} = 0.5$$
Cette valeur n'a en soit aucune signification.
Cependant, c'est en utilisant la formule de $arccos$ qu'elle va prendre toute sa signification.
En effet en utilisant une calculatrice et en mettant le mode Deg (et non Rad), on obtiendra ceci : $$arccos(0.5) = \color{red}{\boxed{\color{black}{ 60^{\circ} }}}$$
Ou encore : $$cos(60) = \color{red}{\boxed{\color{black}{ 0.5 }}}$$
Pour aller plus loin, si on a un angle de $60^{\circ}$ dans un triangle rectangle, alors l'autre cote est egal a $30^{\circ}$.
En effet : $90 + 60 + 30 = 180$.
Ainsi on peut demontrer que : $$arcsin(0.5) = \color{red}{\boxed{\color{black}{ 30^{\circ} }}}$$
Ou encore que : $$sin(30) = \color{red}{\boxed{\color{black}{ 0.5 }}}$$
Et si on veut connaitre la valeur de cet arc de cercle, en radian donc, on devra le convertir en radian.
On sait en effet que : $$180 \, deg = \pi \, rad$$
Donc que : $$1 \, deg = \frac{\pi}{180} \, rad$$
Et que par consequent si on veut avoir la valeur de l'arc de cercle pour $60^\circ$, il faut faire comme ceci : $$60 * 1 \, deg = 60 * \frac{\pi}{180} \, rad$$
Ce qui nous donne : $$60 \, deg = \frac{60\pi}{180} \, rad$$ $$ \Leftrightarrow 60 \, deg = \frac{1\pi}{3} \, rad $$ $$ \Leftrightarrow 60 \, deg = \frac{\pi}{3} \, rad $$
Et si on prend sa calculatrice et qu'on calcule ce que vaut $\frac{\pi}{3}$, on aura l'egalite suivante : $$ arccos(\frac{1}{2}) \, rad = \frac{\pi}{3}$$
Et pour finir, on constate que : $$ arccos(0.5) \, rad \approx 1.0471975512 \, rad = \color{red}{\boxed{\color{black}{ \frac{\pi}{3} \, rad }}}$$ $$ arccos(0.5) \, deg = \color{red}{\boxed{\color{black}{ 60 \, deg }}}$$
Ce raisonnement se retrouve a l'aide du graphique suivant :
clf(1);
h=scf(1);
h.figure_name="Hello :D";
title("Trigonometrie du cercle - Unit circle", "fontsize", 5);
scale=2;
t=[0:0.1:%pi*2]; // from 0 to 2*PI with 0.01 step
x=scale*cos(t); // taking cos(t) allows to follow the circle on X axis
y=scale*sin(t); // taking sin(t) allows to follow the circle on Y axis
// A
xstring(0,-0.3,["$A(0,0)$"])
t1=get("hdl") // gets the handle of the newly created object
t1.font_foreground=6; // changes font properties
t1.font_size=3;
t1.font_angle = 20;
// B
xstring(1,-0.3,["$B(1,0)$"])
t2=get("hdl") // gets the handle of the newly created object
t2.font_foreground=6; // changes font properties
t2.font_size=3;
t2.font_angle = 20;
// C
xstring(1.1,sqrt(3)-0.05,["$C(1,\sqrt{3})$"])
t3=get("hdl") // gets the handle of the newly created object
t3.font_foreground=6; // changes font properties
t3.font_size=3;
t3.font_angle = 340;
// D
xstring(0.1,sqrt(3)-0.05,["$D(0,\sqrt{3})$"])
t3=get("hdl") //gets the handle of the newly created object
t3.font_foreground=6; // changes font properties
t3.font_size=3;
t3.font_angle = 340;
// sqrt(3)
xstring(-0.5,sqrt(3)-0.15,["$\sqrt{3}$"])
t3=get("hdl") //gets the handle of the newly created object
t3.font_foreground=1; // changes font properties
t3.font_size=2;
scaleNeg = -2;
scalePos = +2;
plot2d ( ..
x,..
y,..
style=1,.. // black
rect=[scaleNeg, scaleNeg, scalePos, scalePos],..
frameflag=3,.. // isometrique (perfect cercle)
axesflag=4.. // scale with numbers inside the graphic
);
e0=gce();
e0=e0.children(1);
e0.thickness=1;
//////
scale=2;
t=[0:0.01:1]; // from 0 to 1 with 0.01 step
x=scale*cos(t); // taking cos(t) allows to follow the circle on X axis
y=scale*sin(t); // taking sin(t) allows to follow the circle on Y axis
// =================================================================
// 60
// =================================================================
// ========================== 60 degrees - arc of a circle near (0,0)
plot2d ( ..
x/8,..
y/8,..
style=1,.. // black
rect=[scaleNeg, scaleNeg, scalePos, scalePos],..
frameflag=3,.. // isometrique (perfect cercle)
axesflag=4.. // scale with numbers inside the graphic
);
e0=gce();
e0=e0.children(1);
e0.thickness=1;
// ========================== 60 degrees - arc of a circle bottom
plot2d ( ..
(x/5)-1,..
(y/5)-(sqrt(3)),..
style=1,.. // black
rect=[scaleNeg, scaleNeg, scalePos, scalePos],..
frameflag=3,.. // isometrique (perfect cercle)
axesflag=4.. // scale with numbers inside the graphic
);
e0=gce();
e0=e0.children(1);
e0.thickness=1;
// 60 degrees - 1
xstring(0.25,0.05,["$60^{\circ}$"])
// 60 degrees - 2
xstring(-0.6,-sqrt(3)+0.15,["$60^{\circ}$"])
// sqrt(3)
xstring(1,0.7,["$\sqrt(3)$"])
xstring(1,-0.9,["$\sqrt(3)$"])
// 2
xset("font",1,2); xstring(0.45,0.8,["$2$"], -70)
xset("font",1,2); xstring(-0.45,-0.8,["$2$"], -70)
xset("font", 1, 1);
// =================================================================
// 90
// =================================================================
// ========================= 90 degree - square 1
squareX=0.8;
squareY=0.17;
xs=[[squareX, squareX] , [squareX, 1]],
ys=[[0, squareY] , [squareY, squareY]];
plot2d(xs, ys);
es=gce();
es=es.children(1);
es.thickness=1;
// ========================= 90 degree - square 2
squareX=0.8;
squareY=-sqrt(3);
xs=[[squareX, squareX] , [1, 1]], // from every X1 to X2
ys=[[squareY, squareY + 0.2] , [squareY + 0.2, squareY + 0.2]]; // from every Y1 to Y2
plot2d(xs, ys);
es=gce();
es=es.children(1);
es.thickness=1;
// 90 degrees
xstring(0.6,0.2,["$90^{\circ}$"])
xstring(0.6,-1.55,["$90^{\circ}$"])
// =================================================================
// 30
// =================================================================
// =========================== 30 degrees - arc of circle
// 60 * (pi/180) = pi/3. So pi radian divided by three.
scale=2;
t=[(%pi/3)+%pi:0.01:(3/2)*(%pi)]; // 0.01 step
x=scale*cos(t); // taking cos(t) allows to follow the circle on X axis
y=scale*sin(t); // taking sin(t) allows to follow the circle on Y axis
plot2d ( ..
(x/4)+1,..
(y/4)+1.7,.. // place the arc of circle at the right area
style=1,.. // black
rect=[scaleNeg, scaleNeg, scalePos, scalePos],..
frameflag=3,.. // isometrique (perfect cercle)
axesflag=4.. // scale with numbers inside the graphic
);
es=gce();
es=es.children(1);
es.thickness=1;
// ============================ 30 degrees text
xstring(0.73,1,["$30^{\circ}$"])
// =================================================================
// Arc of circle
// =================================================================
// =========================== Yellow arc
// 60 * (pi/180) = pi/3. So pi radian divided by three.
scale=2;
t=[0:0.01:(%pi)/3]; // 0.01 step
x=scale*cos(t); // taking cos(t) allows to follow the circle on X axis
y=scale*sin(t); // taking sin(t) allows to follow the circle on Y axis
xset("line style", 1); // all lines are normal
xset("font",1,4);xstring(1.8,0.9,["$\frac{\pi}{3}$"], 0);
xset("font",1,1);// font normal
plot2d ( ..
(x),..
(y),.. // place the arc of circle at the right area
style=color(0, 0, 0),.. // color
rect=[scaleNeg, scaleNeg, scalePos, scalePos],..
frameflag=3,.. // isometrique (perfect cercle)
axesflag=4.. // scale with numbers inside the graphic
);
es=gce();
es=es.children(1);
es.thickness=4;
xset("line style", 7); // all lines are dashed
// =================================================================
// Lines
// =================================================================
// Line RED: x = 1 with radius of circle = 2, so y = sqrt(3)
x=[1,1]; y=[-sqrt(3),sqrt(3)]; plot2d(x,y,style=5); e1=gce(); e1=e1.children(1); e1.thickness=2;
x=[-1,-1]; y=[-sqrt(3),sqrt(3)]; plot2d(x,y,style=5); e1=gce(); e1=e1.children(1); e1.thickness=2;
// Line GREEN: x = 0 to 1, y = 0 to sqrt(3)
x=[-1,1]; y=[-sqrt(3),sqrt(3)]; plot2d(x,y,style=3); e2=gce(); e2=e2.children(1); e2.thickness=4;
// Line BLUE: x = 0 to 1, y = sqrt(3)
x=[-1,1]; y=[sqrt(3), sqrt(3)]; plot2d(x,y,style=2); e3=gce(); e3=e3.children(1); e3.thickness=2;
x=[-1,1]; y=[-sqrt(3), -sqrt(3)]; plot2d(x,y,style=2); e3=gce(); e3=e3.children(1); e3.thickness=2;
// Line CROSSES
x=[1:1]; y=[sqrt(3)]; plot2d(x, y, style=-2); e4=gce(); e4=e4.children(1); e4.thickness=1;
x=[0:0]; y=[sqrt(3)]; plot2d(x, y, style=-2); e5=gce(); e5=e5.children(1); e5.thickness=1;
x=[1:1]; y=[0:0]; plot2d(x, y, style=-2); e6=gce(); e6=e6.children(1); e6.thickness=1;
x=[0:0]; y=[0:0]; plot2d(x, y, style=-2); e7=gce(); e7=e7.children(1); e7.thickness=1;
Sinus
C'est la même chose que le cosinus mais sur l'axe des ordonnées.
Le sinus est un point se situant sur l'axe des ordonnées à l'intérieur du cercle.
Il est compris dans le diamètre du cercle.